컴퓨터 네트워크 #9
라우팅 연습 문제
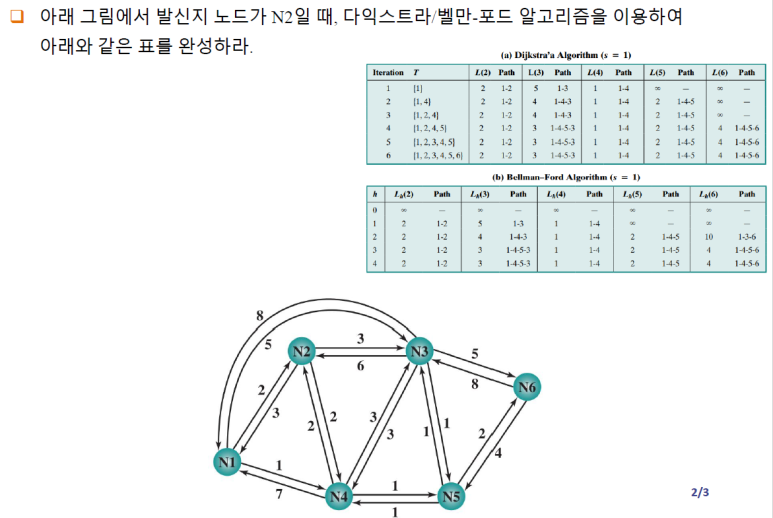
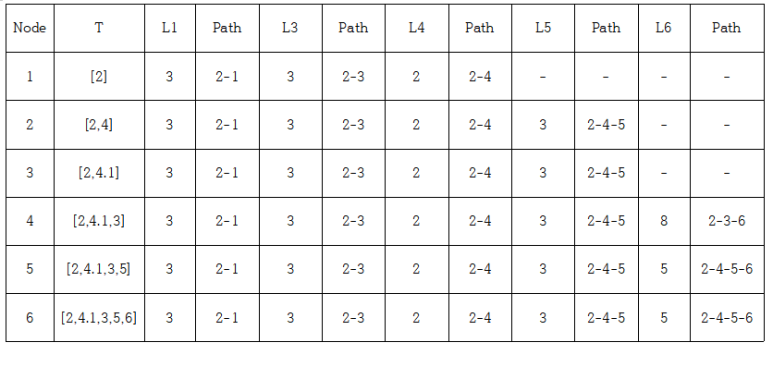
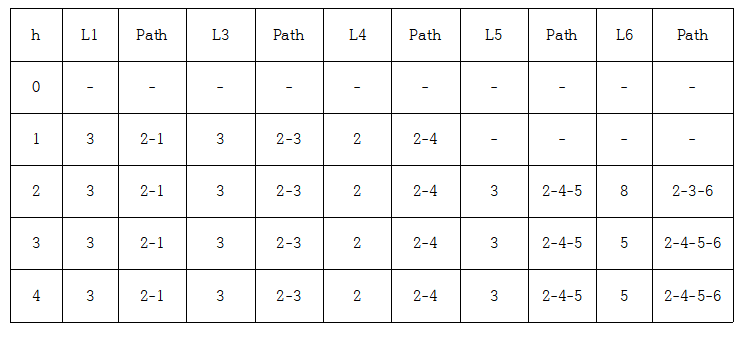
문제 1.
답 1.
다익스트라 알고리즘
벨만 포드 알고리즘
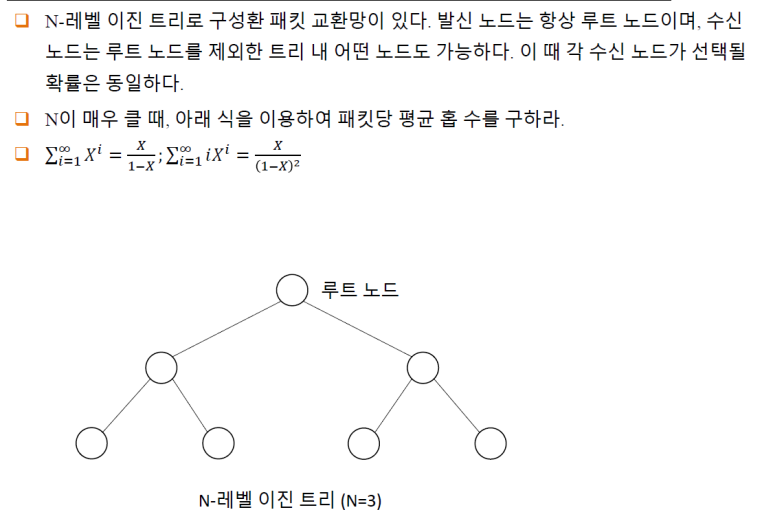
문제 2.
답 2.
답.
N레벨 이진트리의 특징은 다음과 같다.
N레벨 이진트리의 N레벨에 있는 노드 수는 $2^{N-1}$ 개 이다.
ex. 4레벨 이진트리의 4레벨에 있는 노드의 개수는 $2^{4-1} = 8$ 개이다.
N 레벨 이진트리의 N 레벨을 제외한 모든 노드의 수는 $2^{N-1} - 1$ 개 이다.
ex. 4레벨 이진트리의
1~(N-1)레벨까지의 모든 노드의 수는 $2^{4-1} - 1 = 7$ 개이다.루트에서
N레벨 까지 가는데 거쳐가는 경로는N-1이다.ex. 4레벨 이진트리에서 4레벨 노드까지 가는데 거쳐가는 가지(홉 수) 수는 $4-1 = 3$ 가지이다.
N레벨에 있는 노드를 기준으로 보자.
N레벨에 있는 노드의 수는 $2^{n-1}$ 승 개이고, 나머지 모든 노드 수의 합은 그것보다 1개 적다. (1,2번 특징)
n이 무한히 크다고 문제에서 가정했으므로, (N레벨에 있는 노드 수) = (나머지 노드 수)라고 볼 수 있다.
(N이 무한히 크면 1개차이는 무시할 수 있으므로)
따라서 N레벨에 있는 노드가 선택될 확률은 $\frac{1}{2}$ 이다. N레벨 까지가는 데 거치는 홉 수는 N-1개이다.
정리하면 N레벨에 있는 노드가 선택되서 그곳까지 가는 홉수
$= (\frac{1}{2}) \times (N-1)$
N-1레벨에 있는 노드가 선택될 확률은 다시 절반 이므로 $(\frac{1}{2})^2$ 이고 홉수는 N-2가 된다.
이를 루트노드까지 전부 더하면
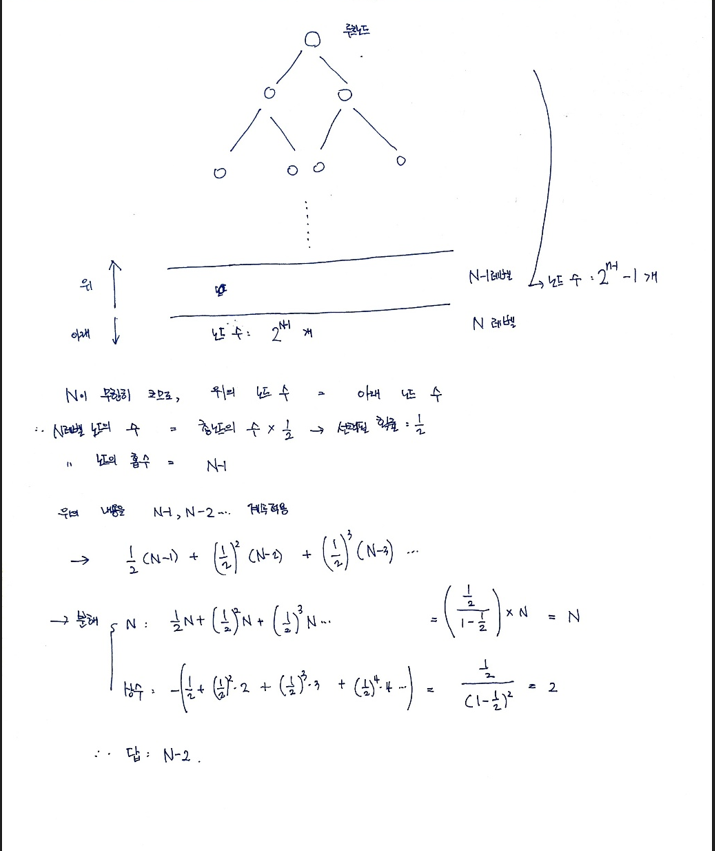
$(\frac{1}{2}) \times (N-1) + (\frac{1}{2})^2 \times (N-2)…$ 이다. 여기서 N은 N끼리 묶고, 상수는 상수끼리 묶어서 문제의 공식을 적용하면 답은 N-2가 된다.
이해를 돕기 위해 아래에 풀이과정을 첨부했다.
