컴퓨터 네트워크 #7

ATM 연습 문제

문제 1.

답 1.

오류가 나는 경우에 대한 문제이다. h+i는 전체 비트수 이고, h는 헤더 비트 수, i는 데이터 비트 수이다.

(헤더 비트 수 / 전체 비트 수 * 한 비트가 오류날 확률) 을 하면 헤더에서 오류가 날 확률이 된다. = hB/(h+i)

(데이터 비트 수 / 전체 비트 수 * 한 비트가 오류날 확률) 을 하면 데이터에서 오류가 날 확률이 된다. = iB/(h+i)

헤더 필드의 오류 비트 수 = hB , 데이터 필드의 오류 비트 수 = iB

문제의 전제조건이 있는데, 풀이는 이 전제조건을 고려해서 작성하였다.

​> 전제 조건 헤더 필드에 오류가 생겨서 잘못전송될 경우 h+i비트만큼 잘못 전송되지만, 이 때 헤더필드는 정보를 담지 않고 있으므로 무시하고 i비트만큼 오류가 발생했다고 계산한다.

오류를 헤더 필드에 오류가 발생할 경우와 발생하지 않을 경우 두 가지로 나눠서 생각해야 한다.

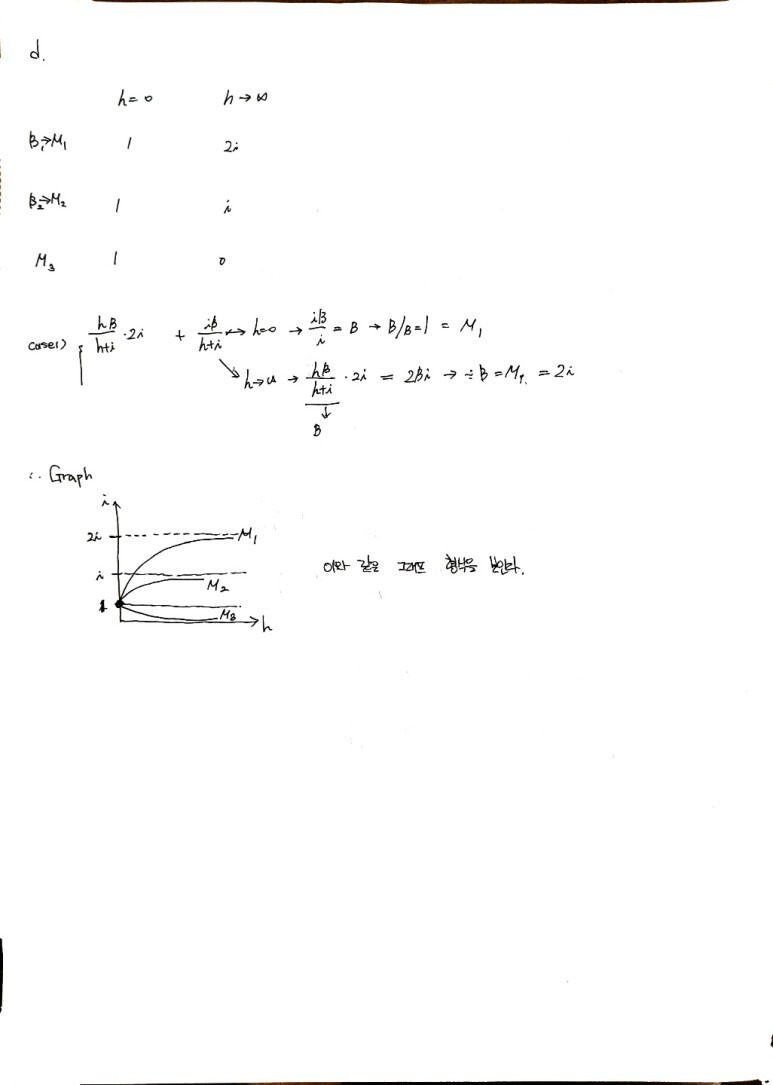
• a의 경우

  헤더필드에 오류가 발생했다.

  → 전체 패킷이 잘못 전송되기 때문에, 원래 수신받아야 하는 목적지는 i비트를 받지 못하고, 엉뚱한 곳에서는 받지 않아도 되는 i비트를 받기 때문에 총 오류비트는 2i비트가 된다.

  이 때 잘못 도착하는 비트 수는 h+i라고 생각되지만, 전제조건에 의해 헤더 필드의 비트는 생각하지 않는다.

  헤더필드에 오류가 발생하지 않았다.

  → 따라서 데이터 필드의 오류 비트 수의 기댓값만 계산하면 된다.

​

• b의 경우

  검출을 했기 때문에, 전송을 하지 않는다.

  → 따라서 엉뚱한 곳으로 잘못 전송되는 경우는 없지만, 원래 받아야 할 곳은 받지 못하기 때문에 오류비트가 i비트 만큼 생긴다.

  헤더필드에 오류가 발생하지 않았다.

  → 데이터 필드의 오류 비트 수의 기댓값만 계산하면 된다.

• c의 경우

  검출에 정정을 했기 때문에, 헤더 필드에는 오류 비트가 단 한개도 없다.

  따라서 헤더필드에 오류가 발생하는 경우는 없다. 따라서 데이터 필드의 오류 비트 수의 기댓값만 계산하면 된다.

풀이에 따라 a,b,c의 경우에 답을 정리하면 아래와 같다.

추가 내용

문제에서 헤더 오류 확률과 데이터 오류확률을 제시하였다. 이 때 헤더 오류 확률을 P , 데이터 오류 확률을 P' 라고 하면, 헤더가 오류나지 않을 확률은 1-P , 데이터에 오류가 없을 확률은 1-P' 로 둘 수 있다.

문제에서 기댓값을 찾으라고 하였으므로, 확률 * 비트 수를 통해서 기댓값을 구할 수 있다.

이 때 헤더와 데이터는 독립적인 필드라고 생각한다.

a번을 보면

• 헤더에 오류가 발생한 경우

  오류확률 * 오류 비트 수를 통해 답을 구할 수 있다.

  헤더의 오류확률은 P이고 헤더의 오류비트 수는 고려하지 않으므로, 추가로 발생한 오류 비트 수는 데이터 필드의 2i 가 된다.

  여기서 데이터 필드의 오류 확률을 전혀 고려할 필요가 없다.

• 헤더에 오류가 없는 경우

  헤더 오류 비트 수는 어차피 0 이므로, 헤더는 전혀 신경쓸 필요가 없다.

  따라서 데이터 오류확률 P' 만 고려하면 된다. 문제에서는 P' 가 이미 오류 비트 수까지 곱해진 확률이라고 제시되어 있다.

문제의 정확한 이해와 풀이를 위해서는 균일 분포에서의 기댓값 계산에 대해 알고 있어야 하는데, 정확히 모르겠다…

문제 자체에서 언급한 헤더 오류 확률과 데이터 오류 확률이 정확하게 무엇을 의미하는 지도 애매모호하고, 기댓값 계산에 어떤 식을 적용한건지도 모르겠다.

그냥 그런가보다 하고 넘어간 문제..

---

문제 2.

답 2.

1. a. 고정길이 셀

   총 필요한 셀의 개수는 $\lceil \frac{X}{L} \rceil$ 개 이다.

   ex. 데이터 크기가 400이고 셀의 데이터 필드 크기가 30이면, 모든 데이터를 전송하려면 $\frac{400}{30} = 13…10$ 이다.

   남은 데이터 10을 버리고 전송할 수 없으므로, 14개의 셀을 전송해야 한다.

   셀의 크기 = 데이터 필드 + 헤더 이므로, L+H 이다.

   정리하면 - 데이터의 크기 = X - 셀의 데이터 크기 = $\lceil \frac{X}{L} \rceil$ - 셀의 개수 = L+H

   N 에 대입하면

   $N = \frac {X}{\lceil \frac{X}{L} \rceil \times (L+H)}$ 가 된다.

​

1. b. 가변길이 셀

   총 필요한 셀의 개수는 1개이다. 셀의 크기 = 총 데이터 크기 + 헤더 크기 + 추가 오버헤드 = $L + H + Hv$

   따라서 N 에 대입하면 $N = \frac{X}{L+H+Hv}$ 가 된다. ​

2. c. 함수 해석

   고정길이 셀의 경우 계산하면 분자는 X, 분모는 $\lceil \frac{X}{48} \rceil \times 53 $ 이다.

   가변길이 셀의 경우 계산하면 분자는 X, 분모는 X+7이다.

   X축 값에는 X를 Y축 값에는 N을 넣고 함수를 그린다.

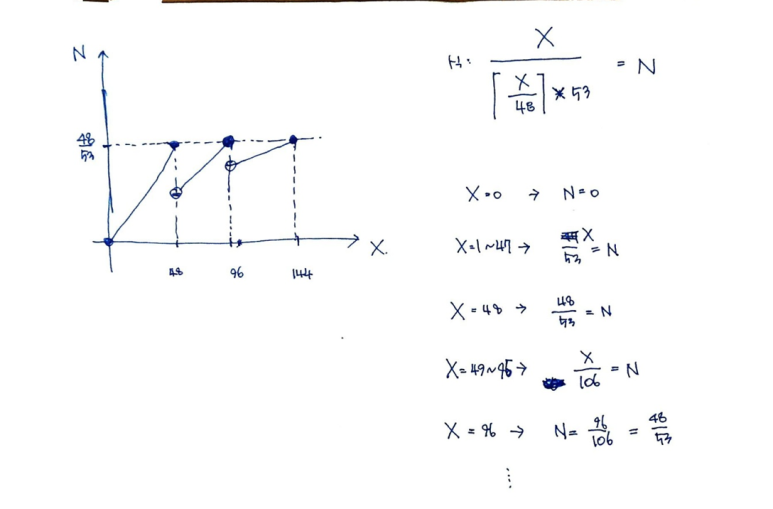
   고정길이 셀의 경우에서 X의 범위를 나눠보면

   X = 1~47 → N = X/53 , X = 49~95 → N = X/106 … 이런식으로 올라가고

   X가 48의 배수일 경우 $\frac{48}{53}$ 이다.

   이를 그래프로 그리면 아래와 같다.

가변길이 셀의 경우 $\frac{X}{X+7}$ 이므로 X=0 일때 N=0이고, X→무한대 일 때, N=1 로 수렴하는 그래프가 그려진다.

두 그래프의 가변길이 셀의 경우 전송률이 더 좋음을 알 수 있다.

하지만 실제로는 셀의 크기가 커짐에 따라 네트워크 혼잡과 지연이 발생하기 때문에, 고정길이 셀이 효율이 더 좋다.

그래서 ATM의 경우 고정길이를 사용한다.

---

문제 3.

답 3.

TIP
위 문제는 셀의 길이를 53옥텟으로 생각해야 한다.
bps = bit per second / BPS = Byte Per Second

​

1. a

   셀의 크기 / 전송율 이 된다.

   따라서 $ \frac{53 \times 8}{43 \times 10^6} (옥텟 = 8bit, M = 10^6 )$ 이다.

   이 값을 X라고 둔다.

​

1. b

   설명에 따르면, 다른 셀이 전송중이면 우선순위가 아무리 높아도 현재 셀이 전송 될 때까지 기다린 후에 전송해야 한다.

   따라서 최대 시간의 경우, 내가 보내는 N번 셀이 도착함과 동시에 교환기에서 M번 셀의 전송을 시작하는 경우이다.

   내 N번 셀은 M번 셀이 다 전송된 후에야 전송을 시작할 수 있다.

   식으로 나타내면 최대시간 = 전송시간 + 최대지연 이다.

   교환기가 5개이고 첫 교환기에 도달한 순간부터 시간을 측정하므로,

   • 1번 교환기 → 2번 : 전송 T, 지연 T
   • 2번 → 3번 : T+T
   • 3번 → 4번 : T+T
   • 4번 → 5번 : T+T
   • 5번 → 종단 : T+T 총 10T 이고 a에서 T=X로 두었으므로, 최대 10X의 시간이 걸린다.

2. c

   전송시간은 변하지 않았으므로 5X 이다.

   교환기가 5개라고 주어졌으므로 단순하게 계산하면 5개의 교환기 중 0.6이 사용중이므로, 3개가 사용중이다.

   3개의 평균시간은 최대의 절반이라고 했으므로, 3개의 교환기의 지연시간은 1.5X 이고 나머지 2개 교환기의 지연시간은 없다.

   따라서 답은 6.5X가 된다.

   • 식 : 지연된 확률 * 지연시간 * 교환기 수

3. d. 지연 변이(지터)는 총 시간 - 전송시간을 말한다. 따라서 b = 5X 이고 c = 1.5X 이다.

---

문제 4.

답 4.

1. 총 1000 Byte 이므로 , 1000 / 48 = 20.33... 총 21개의 셀이 필요하다.
2. 전송 효율 = 메시지 크기/모든 셀들의 크기 = $ \frac{1000}{53 \times 21}$ , (53 = 셀의 크기, 21 = 셀의 개수)