컴퓨터 네트워크 #5

게시 2023/07/15

By Jaemin Park 15 분읽는 시간

패킷 교환 연습 문제

문제 1.

가상 회선을 통해 노드 X에서 Y로 56 옥텟 메시지를 전송하고자 한다.

가상회선은 3개의 중간 노드 a, b, c가 있다.

네트워크 내의 각 패킷은 4 옥텟 헤더의 제어정보가 있다. 아래 각 경우에 전송시간을 구하라.

T : 1 옥텟에 대한 전송시간
지연은 전부 무시한다

전체 메시지가 하나의 패킷으로 전송된다.
메시지를 2개의 패킷으로 나누어 전송한다.
7개의 패킷을 사용하여 메시지를 전송한다.
14개의 패킷을 사용하여 메시지를 전송한다.
위 문제로부터 어떤 결론을 내릴 수 있는가?

답 1.

현재 상황은 다음과 같다.

X → a → b → c → Y : 총 4번 전송

패킷 크기 = 60 (56+4), 패킷 개수 1개
따라서 $60 \times 4 = 240$, 답 : 240T
패킷 크기 = 32 (28 + 4), 패킷 개수 2개
총 시간
1번 패킷이 노드a로 전송되는데 걸리는 시간 + 2번패킷이 X → Y 전송되는데 걸리는 시간
$= 32T + 32T \times 4 = 160T$, 답 : 160T
패킷 크기 = 12 (8+4) , 패킷 개수 : 7개
총 시간
6번 패킷이 노드a로 전송될 때 까지의 시간 + 7번 패킷이 X → Y 전송되는데 걸리는 시간
$= 6 \times 12T + 12T \times 4 = 120T$, 답 : 120T
패킷 크기 = 8(4+4), 패킷 개수 14개
총 시간
13번 패킷이 노드a로 전송될 때 까지의 시간 + 14번 패킷이 X -> Y 전송되는데 걸리는 시간
$= 13 \times 8T + 8T \times 4 = 136T$, 답 : 136T
패킷 크기가 일정크기 까지는 전송시간이 감소하지만, 일정 크기보다 작아질 경우 오히려 전송시간이 증가한다.

문제 2.

교환망에서 다음과 같은 파라미터를 정의한다.

N : 2개의 주어진 종단 스테이션 간의 홉 수
L : 메시지 길이 (비트)
B : 모든 링크의 데이터 전송율 (bps)
P : 고정 패킷 크기 (비트)
H : 패킷당 헤더의 비트
D : 홉당 전파지연 (초)
S : 호 설정시간 (회선교환 및 가상회선) (초)

(a) (N, L, B, P, H, S, D) = (4, 3200, 9600, 1024, 16, 0.2, 0.001)일 때

회선교환, 가상회선, 데이터그램 방식에 대해 종단 간 지연을 계산하라.

확인 응답/처리 지연은 없다고 가정한다.
데이터그램 방식에서 동일한 경로를 거친다고 가정한다.

(b) (a)의 세 기법 중 어느 두 기법이 동일한 지연을 가지기 위한 일반적인 조건을 유도하라.

(총 세 가지 경우 존재 : 회선교환-가상회선, 데이터그램-가상회선, 데이터그램-회선교환)

답 2.

각 기법이 걸리는 시간은 아래와 같다. (응답,처리지연은 무시한다)

회선 교환 = 호 설정시간 + 전파지연 + 메시지 전송시간
데이터그램 = 전파지연 + 모든 패킷이 전달되는 데 걸리는 시간
가상 회선 = 데이터그램 + 호 설정시간

회선교환
- 호 설정시간 = $S$
- 전파지연 = 홉당 D씩 총 N홉 = $N \times D$
- 메시지 전송시간 = 메시지 길이데이터 전송율 = $\frac{L}{B}$
따라서 총 걸리는 시간 = $S + N \times D + \frac{L}{B}$
데이터그램
패킷의 개수
= (메시지 길이 / 패킷의 데이터 크기)
= 메시지 길이 / ( 패킷의 고정크기 - 헤더비트 )
계산하면, $\frac{L}{P-H}$ (올림)
올림하는 이유 데이터가 1비트라도 남으면 패킷을 하나 더 만들어서 전송해야 한다.
패킷이 전달되는데 걸리는 시간
= (패킷의 개수 - 1) x 패킷 하나의 전송시간 + 마지막 패킷이 수신지에 도착하는데 걸리는 시간
패킷 하나의 전송시간 = $\frac{P}{B}$ 이므로, 모든 패킷이 전달되는데 걸리는 시간은
\[= ( \frac{L}{P-H} -1 ) \times \frac{P}{B} + \frac{P}{B} \times N\]
따라서 모든 시간의 합은
\[T = N \times D + ( \frac{L}{P-H} -1 ) \times \frac{P}{B} + \frac{P}{B} \times N\]

가상회선

데이터그램과 동일한 시간 + 호설정지연 = T(데이터그램) + S

(a) 주어진 값들을 다 대입해서 정리하면 된다.

(b)

위에서 구한 각자 시간을 다 = 놓고 남는 변수를 다 0 으로 만들면, 동등해질 조건이 된다.

ex. 가상회선 - 데이터그램

가상회선 = T(데이터그램) + (S/데이터그램) = T

따라서 같은 지연시간이 걸리려면 T+S = T 여야 하므로 S = 0 이면 된다.

호설정지연이 0초일 경우 동일한 지연이 된다.

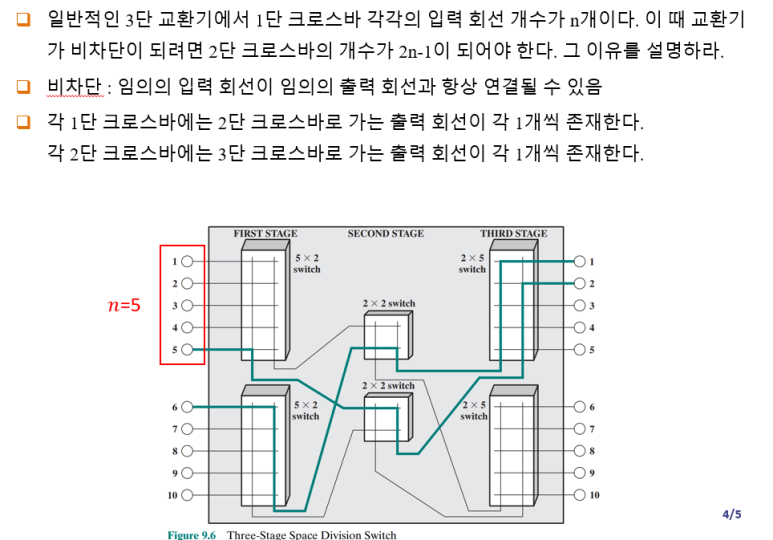
문제 3.

답 3.

1단 교환기의 입력회선이 n개이면, 출력회선도 최소 n개 이상 존재
→ n개의 입력회선이 동시에 다 on 되어도 전부 출력할 수 있어야 하므로
1단 교환기의 출력회선이 n개라면, 2단 교환기의 개수도 최소 n개 이상 존재
→ 출력회선 1개당 2단 교환기 1개랑 매칭되기 때문이다.
(1,2) 번을 가정한 상태에서 1단 교환기가 모두 ON 되었다고 가정하자. 이 때 임의의 입력회선 X를 보자.
1단 교환기에서 입력 회선과 똑같은 수 만큼 출력회선이 있기 때문에, 회선 X가 갈 수 있는 회선은 1개이다.
→ 나머지 N-1개의 출력회선은 회선 X를 제외한, N-1개의 회선이 사용중이다.
2단 교환기를 보면, 입력 회선은 N개이고, 출력회선도 N개, 2단 교환기의 개수도 N개이다.
따라서 X가 사용할 수 있는 회선은 나머지 모든 회선은 N-1개의 회선이 사용중이므로 1개 밖에 없다.
따라서 회선 X가 출력 가능한 곳은 3단 교환기의 출력 회선에서 딱 1군데 밖에 없다.
그렇다면 X가 3단 교환기의 N개의 출력회선을 모두 이용하려면, N-1개의 회선이 더 존재하면 된다.
→ 현재 X가 1개의 회선을 이용가능하므로, N-1개를 추가해주면, 총 N개의 회선을 이용할 수 있고, 3단 교환기의 어디로든지 갈 수 있다.
따라서 원래 가정했던 출력회선의 개수 N개에, N-1개의 회선을 추가했으므로 총 회선의 개수는 2N-1개 이다.
1~8의 결과로 비차단이 되기 위해 필요한 1단 교환기의 출력회선의 수가 최소 2N-1 임을 확인했다.

1단 교환기의 출력회선의 수가 곧 2단 교환기의 개수이다 (문제2번)

따라서 1-9 의 과정을 통해 교환기가 비차단이 되려면 최소 2N-1 개의 2단 교환기가 필요하다는 것을 알 수 있다.

문제 4.

일반적인 3단 교환기의 전체 입/출력 회선 개수가 각각 N개이고, 1단 크로스바의 입력 회선과 3단 크로스바의 출력 회선이 각각 n개라고 하자.

그 결과 1단 크로스바와 3단 크로스바의 개수는 각각 $\frac{N}{n}$개가 된다. 교환기는 비차단이다.

(a) 전체 크로스바 교환기에서 교차점의 총 개수는?

(b) n이 매우 클 때, 비차단 구성을 위한 교차점의 최소 개수를 N의 함수로 구하라

답 4.

(a)

문제의 조건에서 1단 크로스바 와 3단 크로스바의 조건이 완전히 동등하다.

(입출력 회선의 수와 총 크로스 바 교환기의 개수가 동일하므로)

1단 크로스 바 교환기 1개를 보자.

입력 회선은 n개이다. 교환기가 비차단이라고 문제에서 주어졌으므로, 출력회선(=2단 크로스바 교환기 개수)은 2n-1개가 되어야한다.(문제3번 참조)

따라서 교환기 1개의 교차점의 개수는 $n \times (2n-1)$ 이 되고, 총 교환기의 개수가 $\frac{N}{n}$ (문제언급) 이므로

1단 크로스 바 교환기의 총 교차점의 개수는 $n \times (2n-1) \times \frac{N}{n}$이 된다.

2단 크로스 바 교환기 1개를 보자.

1단 교환기에 번호를 매겨보면, 1-1번, 1-2번 … 1-N/n번 이 된다.

2단 교환기 1개는 1단 교환기 1개당 1개의 회선을 받는다.

여기서 2단 교환기 중 첫번째를 2-1번 교환기라고 하자.

그렇다면 2-1번 교환기는 1-1번에서 회선1개, 1-2번에서 회선 1개, …, 1- $\frac{N}{n}$ 번에서 회선 1개를 받는다.

따라서 2-1번 교환기는 $\frac{N}{n}$ 개의 입력회선을 갖게 된다.

문제에서 3단 교환기의 개수도 $\frac{N}{n}$ 개 라고 하였으므로, 2단 교환기의 출력 회선 수도 $\frac{N}{n}$ 개가 된다.

따라서 2단 교환기 1개의 교차점의 수는 $(\frac{N}{n})^2$ 이 된다.

총 2단 교환기의 개수가 2n-1 개 이므로, 2단 교환기의 총 교차점의 수는 $(\frac{N}{n})^2 \times (2n-1)$ 이 된다.

3단 교환기는 1단 교환기와 같은 개수의 교차점을 갖는다.

따라서 총 교차점의 개수
= 1단 교환기의 교차점의 개수 x 2(3단교환기) + 2단 교환기의 교차점의 개수
$= n \times ( 2n-1 ) \times \frac{N}{n} \times 2 + (\frac{N}{n})^2 \times (2n-1)$

(b)

n이 매우크다 → 2n-1과 2n은 같은 값이 된다.

(a) 에서 구한 식에 2n-1 대신 2n을 넣어서 정리하면 $\frac{2}{n} \times (N^2) + 4nN$ 이 된다.

교차점의 개수를 y 라고 두면

\[y = \frac{2}{n} \times (N^2) + 4nN\]

최솟값을 찾아야 하므로 미분 = 0 해서 정리하면 된다.

n에 대해 미분하면

\[4 \times N + \frac{-(2N^2)}{(n^2)} = 0\]

정리하면 $n = \sqrt{\frac{N}{2}}$

$\frac{2}{n} \times (N^2) + 4nN$ 에 대입해서 정리하면

$y = 4N \times \sqrt{2N}$ 이 된다.

Major, Computer Network

컴퓨터 네트워크 Computer Network